Batchelor Cornerflow Example#
Author: Cian Wilson
Description#
As a reminder we are seeking the approximate velocity and pressure solution of the Stokes equation
in a unit square domain, \(\Omega = [0,1]\times[0,1]\).
We apply strong Dirichlet boundary conditions for velocity on all four boundaries
and a constraint on the pressure to remove its null space, e.g. by applying a reference point
Parallel Scaling#
In the previous notebook we tested that the solution of the Batchelor cornerflow problem using our new implementation of the Stokes equation, using a PETSc MATNEST matrix, converged at the same suboptimal rate as our original implementation. We also wish to test for parallel scaling of the new implementation, assessing if the simulation wall time decreases as the number of processors used to solve it is increases.
Here we perform strong scaling tests on our function solve_batchelor_nest from notebooks/02_background/2.4d_batchelor_nest.ipynb.
Preamble#
We start by loading all the modules we will require.
import sys, os
basedir = ''
if "__file__" in globals(): basedir = os.path.dirname(__file__)
path = os.path.join(basedir, os.path.pardir, os.path.pardir, 'python')
sys.path.append(path)
import utils.ipp
from background.batchelor import test_plot_convergence
import matplotlib.pyplot as pl
import pathlib
output_folder = pathlib.Path(os.path.join(basedir, "output"))
output_folder.mkdir(exist_ok=True, parents=True)
Implementation#
We perform the strong parallel scaling test using a utility function (profile_parallel from python/utils/ipp.py) that loops over a list of the number of processors calling our function for a given number of elements, ne, and polynomial order p. It runs our function solve_batchelor a specified number of times and evaluates and returns the time taken for each of a number of requested steps.
# the list of the number of processors we will use
nprocs_scale = [1, 2, 4]
# the number of elements to solve the problem on
ne = 128
# the polynomial degree of our pressure field
p = 1
# perform the calculation a set number of times
number = 1
# We are interested in the time to create the mesh,
# declare the functions, assemble the problem and solve it.
# From our implementation in `solve_poisson_2d` it is also
# possible to request the time to declare the Dirichlet and
# Neumann boundary conditions and the forms.
steps = [
'Mesh', 'Function spaces',
'Assemble', 'Solve',
]
# declare a dictionary to store the times each step takes
maxtimes = {}
Direct (block)#
To start with we test the scaling with the original implementation and the default solver options, which are a direct LU decomposition using the MUMPS library implementation.
maxtimes['Direct (block)'] = utils.ipp.profile_parallel(nprocs_scale, steps, path, 'background.batchelor', 'solve_batchelor',
ne, p, number=number)
=========================
1 2 4
Mesh 0.03 0.03 0.06
Function spaces 0.02 0.02 0.02
Assemble 0.27 0.16 0.14
Solve 1.45 1.3 1.48
=========================
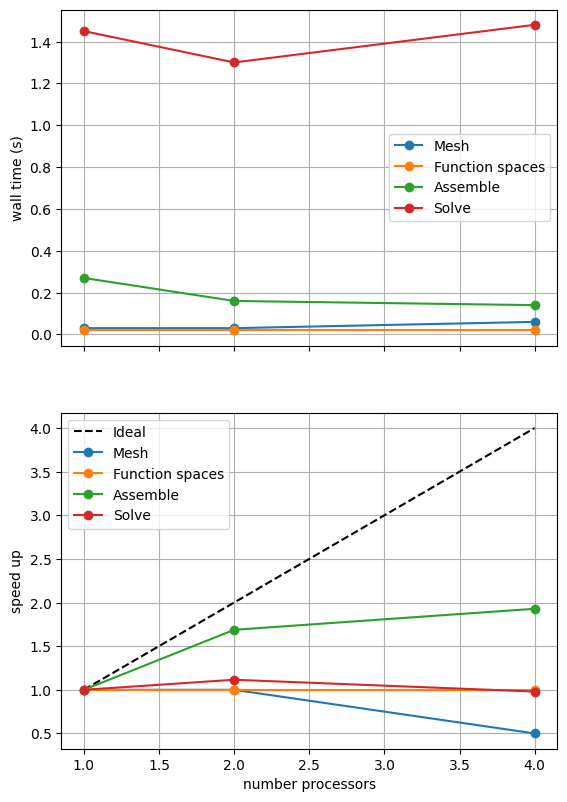
The behavior of the scaling test will strongly depend on the computational resources available on the machine where this notebook is run. In particular when the website is generated it has to run as quickly as possible on github, hence we limit our requested numbers of processors, size of the problem (ne and p) and number of calculations to average over (number) in the default setup of this notebook.
For comparison we provide the output of this notebook using ne = 256, p = 1 and number = 10 in Figure 2.4.2 generated on a dedicated machine with a local conda installation of the software.
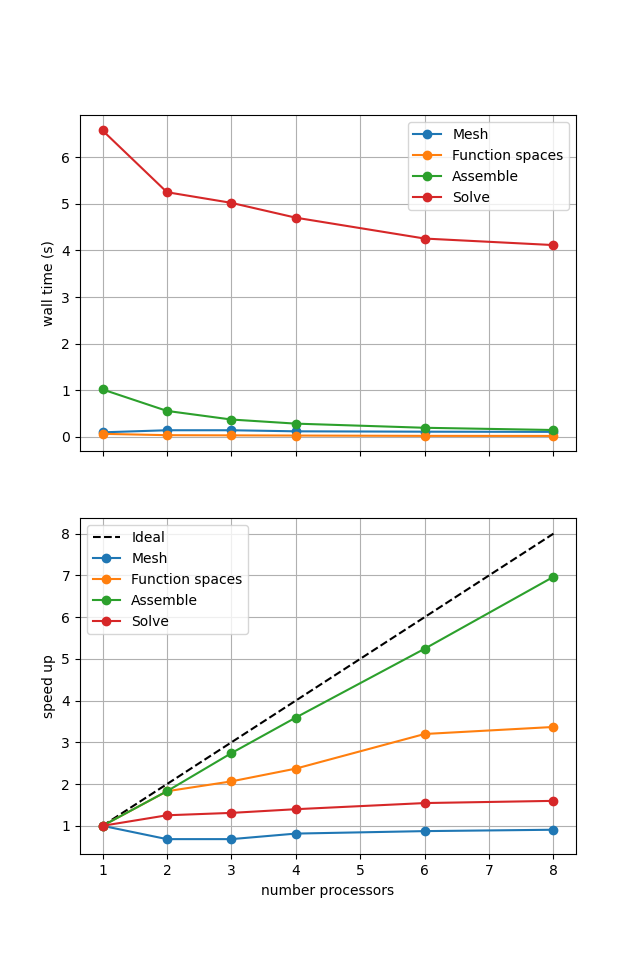
Figure 2.4.2 Scaling results for a direct solver with ne = 256, p = 1 averaged over number = 10 calculations using a local conda installation of the software on a dedicated machine.
We can see in Figure 2.4.2 that assembly and function space declarations scale well, with assembly being almost ideal. However meshing and the solve barely scale at all. As previously discussed, the meshing takes place on a single process before being communicated to the other processors, hence we do not expect this step to scale. Additionally the cost (wall time taken) of meshing is so small that it is not a significant factor in these simulations. The solution step is our most significant cost and would ideally scale.
We have already tested that this implementation converges in parallel so we move onto testing if the new implementation behaves any better.
Direct (nest)#
We test the new implementation, using a PETSc MATNEST matrix with the same default solver options.
maxtimes['Direct (nest)'] = utils.ipp.profile_parallel(nprocs_scale, steps, path, 'background.batchelor_nest', 'solve_batchelor_nest',
ne, p, number=number,
output_filename=output_folder / 'batchelor_scaling_direct_nest.png')
=========================
1 2 4
Mesh 0.03 0.03 0.06
Function spaces 0.02 0.01 0.02
Assemble 0.17 0.11 0.09
Solve 1.55 1.34 1.45
=========================
*********** profiling figure in output/batchelor_scaling_direct_nest.png
If sufficient computational resources are available when running this notebook (unlikely during website generation) this should show similar results to the original version. For comparison we provide the output of this notebook using ne = 256, p = 1 and number = 10 in Figure 2.4.3 generated on a dedicated machine with a local conda installation of the software.
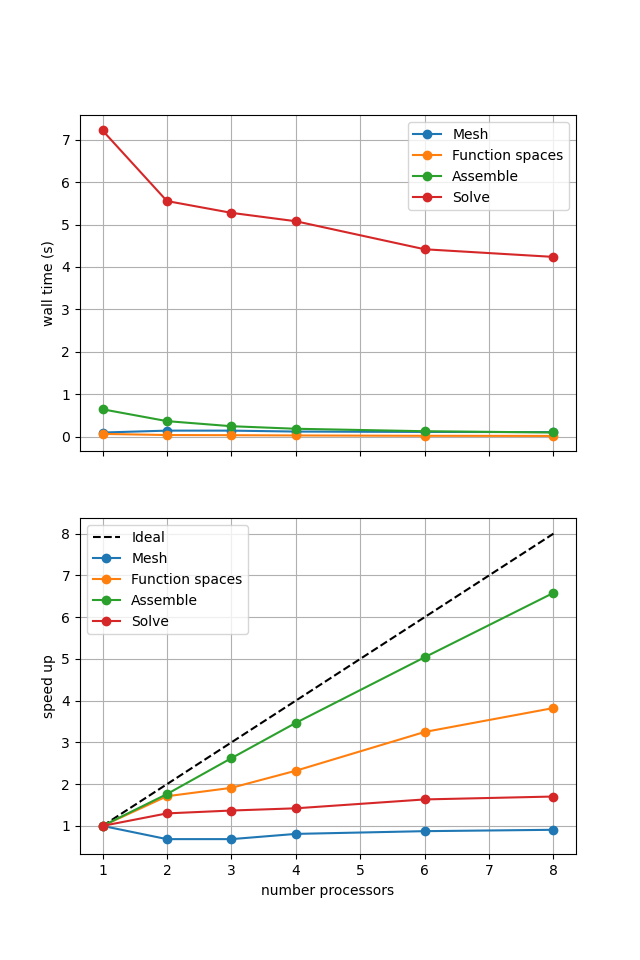
Figure 2.4.3 Scaling results for a direct solver using a MATNEST matrix with ne = 256, p = 1 averaged over number = 10 calculations using a local conda installation of the software on a dedicated machine.
Figure 2.4.3 shows that our new implementation scales in a similar manner to the original when using a direct solver. To double check that it is working we re-run our convergence test in parallel.
# the list of the number of processors to test the convergence on
nprocs_conv = [2,]
# List of polynomial orders to try
ps = [1, 2]
# List of resolutions to try
nelements = [10, 20, 40, 80]
errors_l2_all = utils.ipp.run_parallel(nprocs_conv, path, 'background.batchelor_nest', 'convergence_errors_nest', ps, nelements)
for errors_l2 in errors_l2_all:
test_passes = test_plot_convergence(ps, nelements, errors_l2)
assert(test_passes)
order of accuracy p=1, order=1.0000050785210868
order of accuracy p=2, order=0.9999999771173882
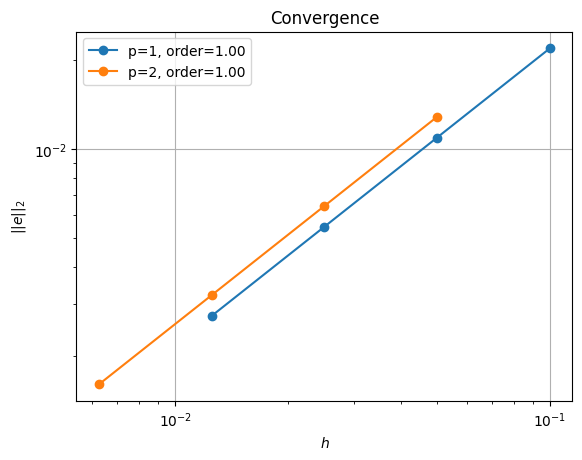
Which does scale (suboptimally) as expected.
Iterative (nest, refpt)#
Unlike the original implementation, we should be able to use an iterative solver (e.g., minres) on the new implementation. We do this by applying a fieldsplit preconditioner using a pressure mass matrix to precondition the zero saddle point block of the Stokes problem.
petsc_options = {'ksp_type':'minres',
'pc_type':'fieldsplit',
'pc_fieldsplit_type': 'additive',
'fieldsplit_v_ksp_type':'preonly',
'fieldsplit_v_pc_type':'gamg',
'fieldsplit_p_ksp_type':'preonly',
'fieldsplit_p_pc_type':'jacobi'}
maxtimes['Iterative (nest, refpt)'] = utils.ipp.profile_parallel(nprocs_scale, steps, path, 'background.batchelor_nest', 'solve_batchelor_nest',
ne, p, number=number, petsc_options=petsc_options,
output_filename=output_folder / 'batchelor_scaling_iterative_refpt.png')
=========================
1 2 4
Mesh 0.03 0.04 0.06
Function spaces 0.02 0.01 0.01
Assemble 0.21 0.12 0.12
Solve 2.83 1.7 1.53
=========================
*********** profiling figure in output/batchelor_scaling_iterative_refpt.png
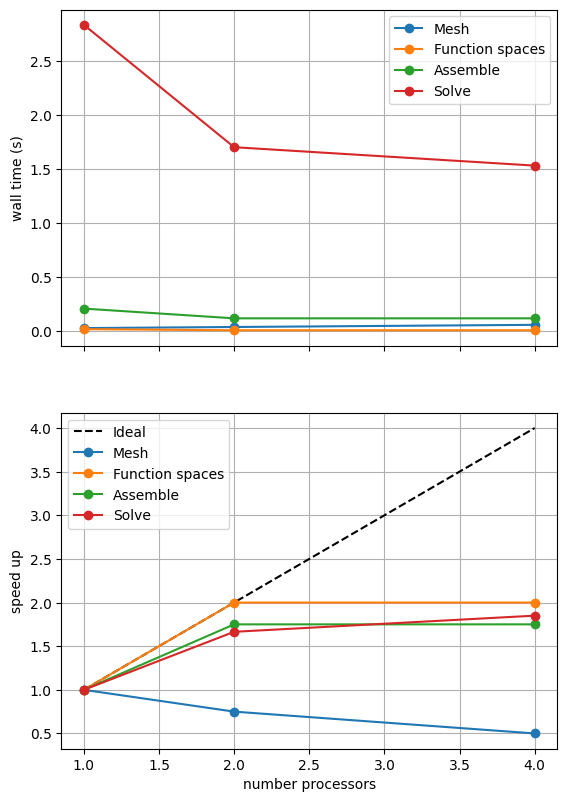
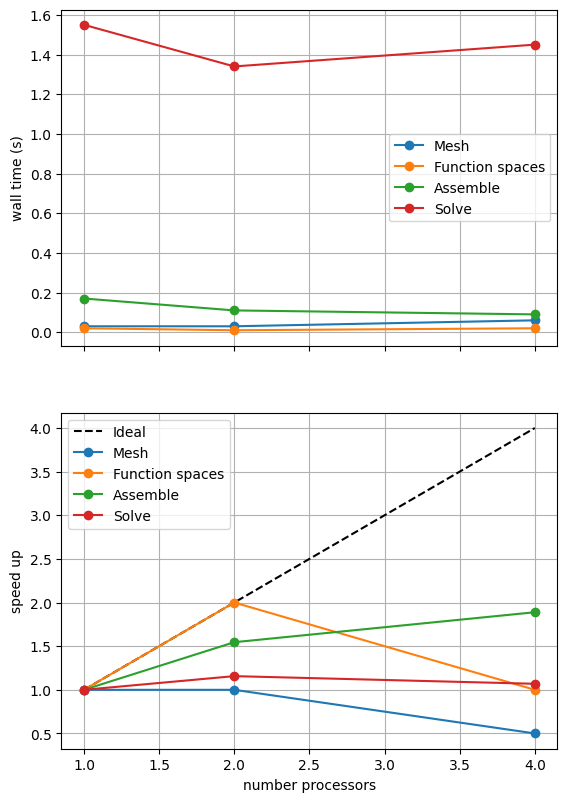
If sufficient computational resources are available when running this notebook (unlikely during website generation) this should show that the scaling (“speed up”) of our solve step has improved but the overall wall time appears larger than when using a direct (LU) solver. For comparison we provide the output of this notebook using ne = 256, p = 1 and number = 10 in Figure 2.4.4 generated on a dedicated machine with a local conda installation of the software.
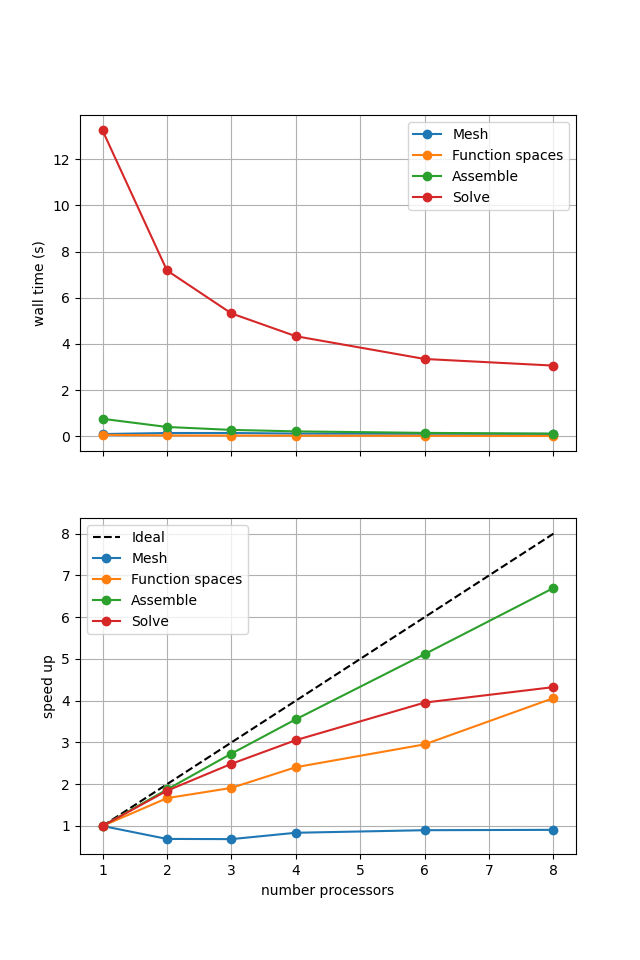
Figure 2.4.4 Scaling results for a direct solver using a MATNEST matrix with ne = 256, p = 1 averaged over number = 10 calculations using a local conda installation of the software on a dedicated machine.
Figure 2.4.4 indeed shows that the scaling (“speed up”) of our solve step has improved but the overall wall time appears larger than when using a direct (LU) solver. As before, we double check our solution is converging in parallel using these solver options.
errors_l2_all = utils.ipp.run_parallel(nprocs_conv, path, 'background.batchelor_nest', 'convergence_errors_nest', ps, nelements, petsc_options=petsc_options)
for errors_l2 in errors_l2_all:
test_passes = test_plot_convergence(ps, nelements, errors_l2)
assert(test_passes)
order of accuracy p=1, order=1.0002187815519132
order of accuracy p=2, order=1.0026912368570127
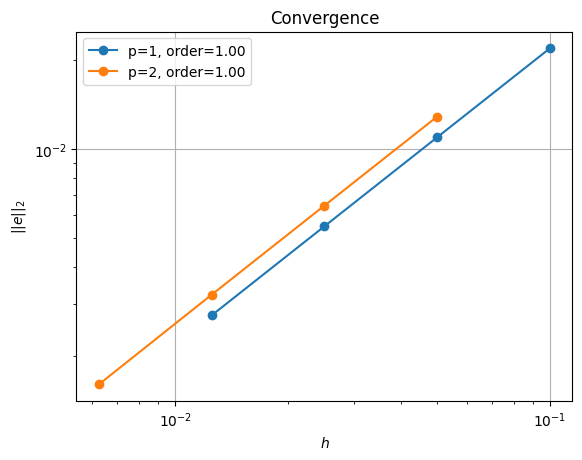
Iterative (nest, null space)#
Our new implementation also allows us to try another method of dealing with the pressure nullspace - removing the null space at each iteration of the solver rather than imposing a reference point. We can test this method by setting the attach_nullspace flag to True.
petsc_options = {'ksp_type':'minres',
'pc_type':'fieldsplit',
'pc_fieldsplit_type': 'additive',
'fieldsplit_v_ksp_type':'preonly',
'fieldsplit_v_pc_type':'gamg',
'fieldsplit_p_ksp_type':'preonly',
'fieldsplit_p_pc_type':'jacobi'}
maxtimes['Iterative (nest, ns)'] = utils.ipp.profile_parallel(nprocs_scale, steps, path, 'background.batchelor_nest', 'solve_batchelor_nest',
ne, p, number=number, petsc_options=petsc_options, attach_nullspace=True,
output_filename=output_folder / 'batchelor_scaling_iterative_ns.png')
=========================
1 2 4
Mesh 0.03 0.04 0.08
Function spaces 0.02 0.01 0.01
Assemble 0.19 0.12 0.11
Solve 1.53 0.98 0.86
=========================
*********** profiling figure in output/batchelor_scaling_iterative_ns.png
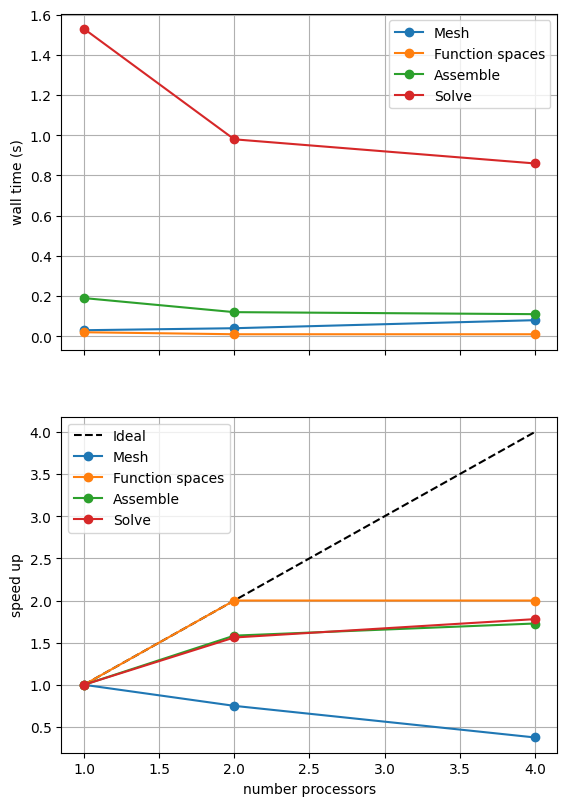
If sufficient computational resources are available when running this notebook (unlikely during website generation) this should show a substantial reduction in the cost of our solution while maintaining reasonable scaling (“speed up”) at this problem size. For comparison we provide the output of this notebook using ne = 256, p = 1 and number = 10 in Figure 2.4.5 generated on a dedicated machine with a local conda installation of the software.
Figure 2.4.5 Scaling results for a direct solver using a MATNEST matrix with ne = 256, p = 1 averaged over number = 10 calculations using a local conda installation of the software on a dedicated machine.
Figure 2.4.5 indeed shows a substantially lower cost while also scaling reasonably well. Again, we double check our solution is converging in parallel using these solver options.
errors_l2_all = utils.ipp.run_parallel(nprocs_conv, path, 'background.batchelor_nest', 'convergence_errors_nest', ps, nelements, petsc_options=petsc_options, attach_nullspace=True)
for errors_l2 in errors_l2_all:
test_passes = test_plot_convergence(ps, nelements, errors_l2)
assert(test_passes)
order of accuracy p=1, order=0.9126715734780724
order of accuracy p=2, order=0.9274958545683684
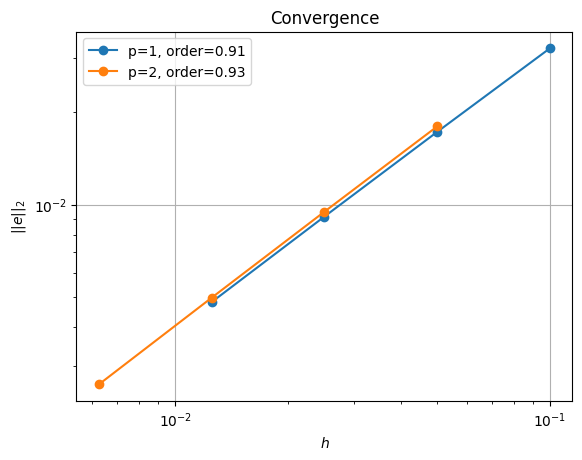
We see that we are converging but at a slightly lower rate than using the reference point.
Comparison#
We can more easily compare the different solution method directly by plotting their walltimes for assembly and solution.
# choose which steps to compare
compare_steps = ['Assemble', 'Solve']
# set up a figure for plotting
fig, axs = pl.subplots(nrows=len(compare_steps), figsize=[6.4,4.8*len(compare_steps)], sharex=True)
if len(compare_steps) == 1: axs = [axs]
for i, step in enumerate(compare_steps):
s = steps.index(step)
for name, lmaxtimes in maxtimes.items():
axs[i].plot(nprocs_scale, [t[s] for t in lmaxtimes], 'o-', label=name)
axs[i].set_title(step)
axs[i].legend()
axs[i].set_ylabel('wall time (s)')
axs[i].grid()
axs[-1].set_xlabel('number processors')
# save the figure
fig.savefig(output_folder / 'batchelor_scaling_comparison.png')
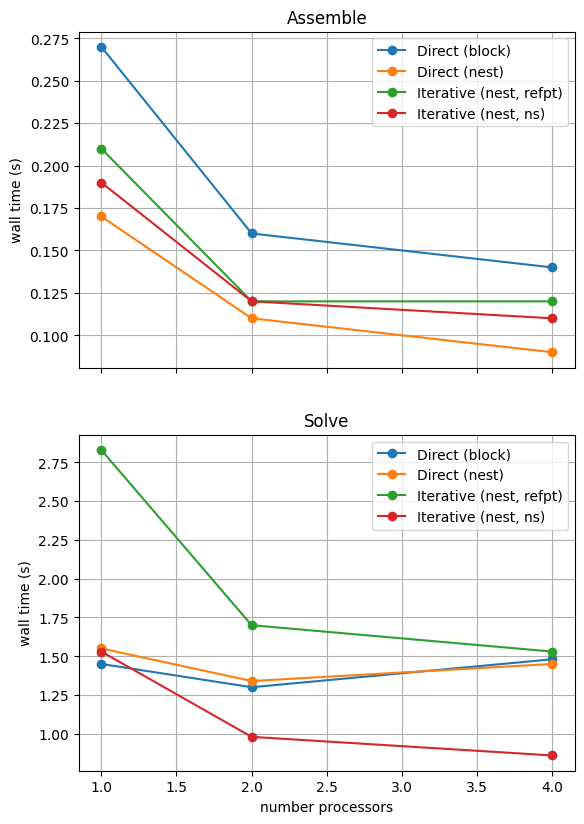
With sufficient computational resources we will see that the MATNEST approach has lowered our assembly costs, though as this is such a small overall part of our wall time it doesn’t make a big impact in this case. However, the decreased cost and improved scaling of the iterative solver method (removing the nullspace iteratively) makes a substantial difference to the cost of our solution. We provide the output of this notebook using ne = 256, p = 1 and number = 10 in Figure 2.4.6 generated on a dedicated machine with a local conda installation of the software.
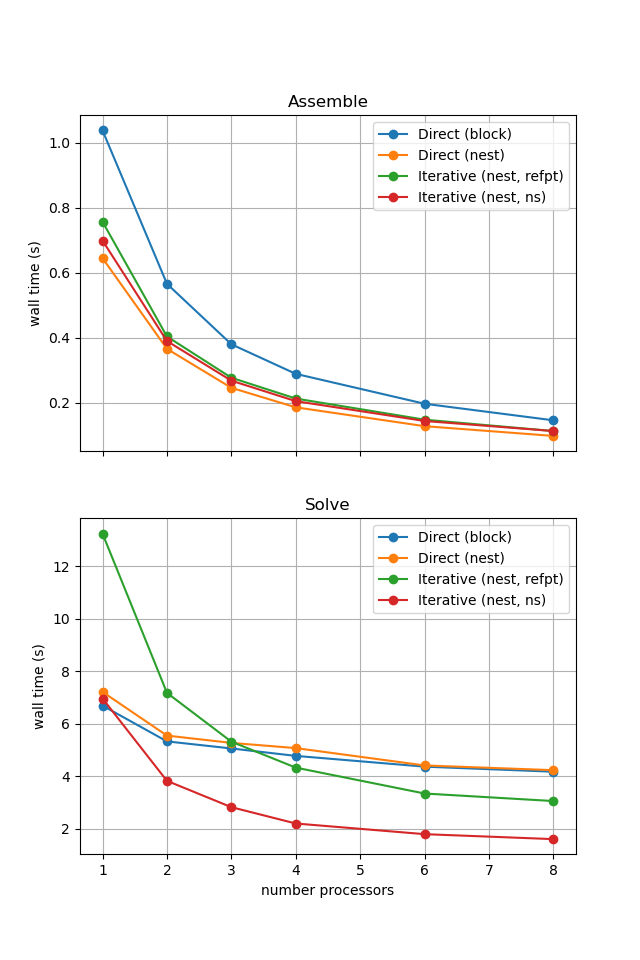
Figure 2.4.6 Comparison of scaling results for different solution strategies with ne = 256, p = 1 averaged over number = 10 calculations using a local conda installation of the software on a dedicated machine.
In the next example we will see how the advantage of using the iterative method is removed at these problem sizes when we have to solve the equations multiple times.
