Batchelor Cornerflow Example#
Author: Cian Wilson
Description#
As a reminder we are seeking the approximate velocity and pressure solution of the Stokes equation
in a unit square domain, \(\Omega = [0,1]\times[0,1]\).
We apply strong Dirichlet boundary conditions for velocity on all four boundaries
and a constraint on the pressure to remove its null space, e.g. by applying a reference point
Solver Requirements#
In the previous notebook we found that our default solution algorithm didn’t scale well in parallel. In the Poisson 2D we fixed this by switching to an iterative solver. To be able to do that for the Stokes system we need a solver that can
precondition a saddle point system with a zero pressure block
precondition each block of the matrix individually to get improved convergence
deal with the pressure null space
These requirements mean that we must modify our implementation of our Batchelor solution algorithm. We choose to do this using a PETSc MATNEST matrix that most easily and efficiently allows us to treat each block of the coupled matrix separately. We additionally add the option to remove the pressure null space at each iteration of the iterative solver rather than imposing a reference point on the pressure solution. For alternative setups for solving the Stokes system we recommend looking at the Stokes demo from FEniCS.
Preamble#
We start by loading all the modules we will require.
from mpi4py import MPI
import dolfinx as df
import dolfinx.fem.petsc
from petsc4py import PETSc
import ufl
import sys, os
basedir = ''
if "__file__" in globals(): basedir = os.path.dirname(__file__)
path = os.path.join(basedir, os.path.pardir, os.path.pardir, 'python')
sys.path.append(path)
import utils.ipp
import utils.plot
from background.batchelor import (unit_square_mesh,
functionspaces,
velocity_bcs,
pressure_bcs,
stokes_weakforms,
dummy_pressure_weakform,
evaluate_error,
test_plot_convergence)
import pathlib
output_folder = pathlib.Path(os.path.join(basedir, "output"))
output_folder.mkdir(exist_ok=True, parents=True)
Implementation#
Our modifications to the solution strategy require us to:
describe a weak form for a pressure pre-conditioner matrix, for which we use a pressure mass matrix - this pre-conditioner matrix has to be different to the coupled system matrix owing to the zero block in the saddle-point system
def pressure_preconditioner_weakform(V_p):
"""
A python function to return a weak form for the pressure preconditioner of
the Stokes problem.
Parameters:
* V_p - pressure function space
Returns:
* M - a bilinear form for the pressure preconditioner
"""
with df.common.Timer("Forms"):
# Grab the mesh
mesh = V_p.mesh
# Define the trial function for the pressure
p_a = ufl.TrialFunction(V_p)
# Define the test function for the pressure
p_t = ufl.TestFunction(V_p)
# Define the integrals to be assembled into a pressure mass matrix
M = df.fem.form(p_t*p_a*ufl.dx)
return M
define a new assembly function to return a nested matrix and (optionally) a preconditioner matrix
def assemble_nest(S, f, bcs, M=None, attach_nullspace=False, attach_nearnullspace=True):
"""
A python function to assemble the forms into a nested matrix and vector.
Parameters:
* S - Stokes form
* f - RHS form
* bcs - list of boundary conditions
* M - pressure mass matrix form (optional, defaults to None)
* attach_nullspace - attach the pressure nullspace to the matrix (optional, defaults to False)
* attach_nearnullspace - attach the possible (near) velocity nullspaces to the preconditioning matrix
(optional, defaults to True)
Returns:
* Sm - a matrix
* Pm - preconditioner matrix (None if M is None)
* fm - a vector
"""
with df.common.Timer("Assemble"):
# assemble the matrix
Sm = df.fem.petsc.assemble_matrix_nest(S, bcs=bcs)
Sm.assemble()
# set a flag to indicate that the velocity block is
# symmetric positive definite (SPD)
Sm00 = Sm.getNestSubMatrix(0, 0)
Sm00.setOption(PETSc.Mat.Option.SPD, True)
# assemble the RHS vector
fm = df.fem.petsc.assemble_vector_nest(f)
# apply the boundary conditions
df.fem.petsc.apply_lifting_nest(fm, S, bcs=bcs)
# update the ghost values
for fm_sub in fm.getNestSubVecs():
fm_sub.ghostUpdate(addv=PETSc.InsertMode.ADD, mode=PETSc.ScatterMode.REVERSE)
bcs_by_block = df.fem.bcs_by_block(df.fem.extract_function_spaces(f), bcs)
df.fem.petsc.set_bc_nest(fm, bcs_by_block)
# assemble the pre-conditioner (if M was supplied)
Pm = None
if M is not None:
Mm = df.fem.petsc.assemble_matrix(M, bcs=bcs_by_block[1])
Mm.assemble()
Pm = PETSc.Mat().createNest([[Sm.getNestSubMatrix(0, 0), None], [None, Mm]])
# set the SPD flag on the diagonal blocks of the preconditioner
Pm00, Pm11 = Pm.getNestSubMatrix(0, 0), Pm.getNestSubMatrix(1, 1)
Pm00.setOption(PETSc.Mat.Option.SPD, True)
Pm11.setOption(PETSc.Mat.Option.SPD, True)
if attach_nearnullspace:
# attach near null spaces to the velocity block
# of the preconditioner matrix
V_v_cpp = df.fem.extract_function_spaces(f)[0]
bs = V_v_cpp.dofmap.index_map_bs
length0 = V_v_cpp.dofmap.index_map.size_local
ns_basis = [df.la.vector(V_v_cpp.dofmap.index_map, bs=bs, dtype=PETSc.ScalarType) for i in range(3)]
ns_arrays = [ns_b.array for ns_b in ns_basis]
dofs = [V_v_cpp.sub([i]).dofmap.map().flatten() for i in range(bs)]
# Set the three translational rigid body modes
for i in range(2):
ns_arrays[i][dofs[i]] = 1.0
x = V_v_cpp.tabulate_dof_coordinates()
dofs_block = V_v_cpp.dofmap.map().flatten()
x0, x1 = x[dofs_block, 0], x[dofs_block, 1]
ns_arrays[2][dofs[0]] = -x1
ns_arrays[2][dofs[1]] = x0
df.la.orthonormalize(ns_basis)
ns_basis_petsc = [PETSc.Vec().createWithArray(ns_b[: bs * length0], bsize=bs, comm=V_v_cpp.mesh.comm) for ns_b in ns_arrays]
nns = PETSc.NullSpace().create(vectors=ns_basis_petsc, comm=V_v_cpp.mesh.comm)
Pm00.setNearNullSpace(nns)
if attach_nullspace:
V_p_cpp = df.fem.extract_function_spaces(f)[1]
# set up a null space vector indicating the null space
# in the pressure DOFs
null_vec = df.fem.petsc.create_vector_nest(f)
null_vecs = null_vec.getNestSubVecs()
null_vecs[0].set(0.0)
null_vecs[1].set(1.0)
null_vec.normalize()
nsp = PETSc.NullSpace().create(vectors=[null_vec], comm=V_p_cpp.mesh.comm)
# test the null space is actually a null space
assert(nsp.test(Sm))
Sm.setNullSpace(nsp)
with df.common.Timer("Cleanup"):
if attach_nullspace: null_vec.destroy()
if M is not None and attach_nearnullspace:
for ns_b_p in ns_basis_petsc: ns_b_p.destroy()
nns.destroy()
return Sm, Pm, fm
define a new solve function to solve a nested matrix allowing preconditioning options to be set on each block using a “fieldsplit” preconditioner
def solve_nest(Sm, fm, V_v, V_p, Pm=None):
"""
A python function to solve a nested matrix vector system.
Parameters:
* Sm - matrix
* fm - vector
* V_v - velocity function space
* V_p - pressure function space
* Pm - preconditioner matrix (optional, defaults to None)
Returns:
* v_i - velocity solution function
* p_i - pressure solution function
"""
# retrieve the petsc options
opts = PETSc.Options()
pc_type = opts.getString('pc_type')
with df.common.Timer("Solve"):
solver = PETSc.KSP().create(MPI.COMM_WORLD)
solver.setOperators(Sm, Pm)
solver.setFromOptions()
# a fieldsplit preconditioner allows us to precondition
# each block of the matrix independently but we first
# have to set the index sets (ISs) of the DOFs on which
# each block is defined
if pc_type == "fieldsplit":
iss = Pm.getNestISs()
solver.getPC().setFieldSplitIS(("v", iss[0][0]), ("p", iss[0][1]))
# Set up the solution functions
v_i = df.fem.Function(V_v)
p_i = df.fem.Function(V_p)
# Create a solution vector and solve the system
x = PETSc.Vec().createNest([v_i.x.petsc_vec, p_i.x.petsc_vec])
solver.solve(fm, x)
# Update the ghost values
v_i.x.scatter_forward()
p_i.x.scatter_forward()
with df.common.Timer("Cleanup"):
solver.destroy()
x.destroy()
if pc_type == "fieldsplit":
for isl in iss[0]: isl.destroy()
return v_i, p_i
Finally we set up a python function, solve_batchelor_nest, that brings these steps together with the unchanged functions from solver_batchelor.
def solve_batchelor_nest(ne, p=1, U=1, petsc_options=None, attach_nullspace=False, attach_nearnullspace=True):
"""
A python function to solve a two-dimensional corner flow
problem on a unit square domain.
Parameters:
* ne - number of elements in each dimension
* p - polynomial order of the pressure solution (optional, defaults to 1)
* U - convergence speed of lower boundary (optional, defaults to 1)
* petsc_options - a dictionary of petsc options to pass to the solver
(optional, defaults to an LU direct solver using the MUMPS library)
* attach_nullspace - flag indicating if the null space should be removed
iteratively rather than using a pressure reference point
(optional, defaults to False)
* attach_nearnullspace - flag indicating if the preconditioner should be made
aware of the possible (near) nullspaces in the velocity
(optional, defaults to True)
Returns:
* v_i - velocity solution function
* p_i - pressure solution function
"""
# 0. Set some default PETSc options
if petsc_options is None:
petsc_options = {"ksp_type": "preonly", \
"pc_type": "lu",
"pc_factor_mat_solver_type": "mumps"}
# and load them into the PETSc options system
opts = PETSc.Options()
for k, v in petsc_options.items(): opts[k] = v
pc_type = opts.getString('pc_type')
# 1. Set up a mesh
mesh = unit_square_mesh(ne)
# 2. Declare the appropriate function spaces
V_v, V_p = functionspaces(mesh, p)
# 3. Collect all the boundary conditions into a list
bcs = velocity_bcs(V_v, U=U)
# We only require the pressure bc if we're not attaching the nullspace
if not attach_nullspace: bcs += pressure_bcs(V_p)
# 4. Declare the weak forms
S, f = stokes_weakforms(V_v, V_p)
# If not attaching the nullspace, include a dummy zero pressure mass
# matrix to allow us to set a pressure constraint
if not attach_nullspace: S[1][1] = dummy_pressure_weakform(V_p)
# If we're not using a direct LU method we need to set up
# a weak form for the pressure preconditioner block (also a
# pressure mass matrix
M = None
if pc_type != "lu": M = pressure_preconditioner_weakform(V_p)
# 5. Assemble the matrix equation (now using _nest)
Sm, Pm, fm = assemble_nest(S, f, bcs, M=M, attach_nullspace=attach_nullspace, attach_nearnullspace=attach_nearnullspace)
# 6. Solve the matrix equation (now using _nest)
v_i, p_i = solve_nest(Sm, fm, V_v, V_p, Pm=Pm)
with df.common.Timer("Cleanup"):
Sm.destroy()
if Pm is not None: Pm.destroy()
fm.destroy()
return v_i, p_i
Let’s check that we can now numerically solve the equations using the new function. With the default options we should still be using a direct LU solver, just with a new nested matrix format.
ne = 10
p = 1
U = 1
v, p = solve_batchelor_nest(ne, p=p, U=U)
v.name = "Velocity"
And visualize the result.
plotter = utils.plot.plot_mesh(v.function_space.mesh, gather=True, show_edges=True, style="wireframe")
utils.plot.plot_vector_glyphs(v, plotter=plotter, gather=True, factor=0.3)
utils.plot.plot_show(plotter)
utils.plot.plot_save(plotter, output_folder / 'batchelor_solution_nest.png')
We can also perform a convergence test of the new implementation to check the solution is still correct.
def convergence_errors_nest(ps, nelements, U=1, petsc_options=None, attach_nullspace=False, attach_nearnullspace=True):
"""
A python function to run a convergence test of a two-dimensional corner flow
problem on a unit square domain.
Parameters:
* ps - a list of pressure polynomial orders to test
* nelements - a list of the number of elements to test
* U - convergence speed of lower boundary (optional, defaults to 1)
* petsc_options - a dictionary of petsc options to pass to the solver
(optional, defaults to an LU direct solver using the MUMPS library)
* attach_nullspace - whether to remove the null space iteratively (optional, defaults to False)
* attach_nearnullspace - flag indicating if the preconditioner should be made
aware of the possible (near) nullspaces in the velocity
(optional, defaults to True)
Returns:
* errors_l2 - a list of l2 errors
"""
errors_l2 = []
# Loop over the polynomial orders
for p in ps:
# Accumulate the errors
errors_l2_p = []
# Loop over the resolutions
for ne in nelements:
# Solve the 2D Batchelor corner flow problem
v_i, p_i = solve_batchelor_nest(ne, p=p, U=U,
petsc_options=petsc_options,
attach_nullspace=attach_nullspace,
attach_nearnullspace=attach_nearnullspace)
# Evaluate the error in the approximate solution
l2error = evaluate_error(v_i, U=U)
# Print to screen and save if on rank 0
if MPI.COMM_WORLD.rank == 0:
print('p={}, ne={}, l2error={}'.format(p, ne, l2error))
errors_l2_p.append(l2error)
if MPI.COMM_WORLD.rank == 0:
print('*************************************************')
errors_l2.append(errors_l2_p)
return errors_l2
# List of polynomial orders to try
ps = [1, 2]
# List of resolutions to try
nelements = [10, 20, 40, 80, 160]
errors_l2 = convergence_errors_nest(ps, nelements)
test_passes = test_plot_convergence(ps, nelements, errors_l2,
output_basename=output_folder / 'batchelor_convergence_nest')
assert(test_passes)
p=1, ne=10, l2error=0.021921089471662037
p=1, ne=20, l2error=0.010960435556187075
p=1, ne=40, l2error=0.005480211135211741
p=1, ne=80, l2error=0.0027401051388757816
p=1, ne=160, l2error=0.0013700525406580791
*************************************************
p=2, ne=10, l2error=0.012877716729228609
p=2, ne=20, l2error=0.0064388586951979665
p=2, ne=40, l2error=0.003219429351274253
p=2, ne=80, l2error=0.0016097146756471187
p=2, ne=160, l2error=0.0008048573378448104
*************************************************
order of accuracy p=1, order=1.0000034726074625
order of accuracy p=2, order=0.9999999846814445
*********** convergence figure in output/batchelor_convergence_nest.pdf
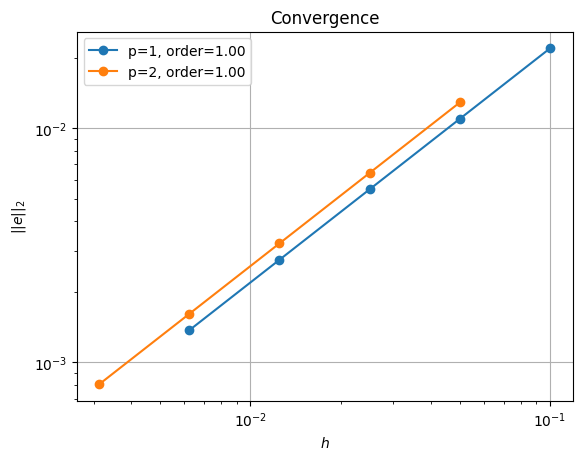
This shows the same (suboptimal) rate of convergence as we saw in the original implementation. Next we will test if our new solver strategy performs any better when we time its performance.
Finish up#
Convert this notebook to a python module (saving first and ignoring markdown cells and those tagged as “main” or “ipy”).
from ipylab import JupyterFrontEnd
app = JupyterFrontEnd()
app.commands.execute('docmanager:save')
!jupyter nbconvert --TagRemovePreprocessor.enabled=True --TagRemovePreprocessor.remove_cell_tags="['main', 'ipy']" --TemplateExporter.exclude_markdown=True --TemplateExporter.exclude_input_prompt=True --TemplateExporter.exclude_output_prompt=True --NbConvertApp.export_format=script --ClearOutputPreprocessor.enabled=True --FilesWriter.build_directory=../../python/background --NbConvertApp.output_base=batchelor_nest 2.4d_batchelor_nest.ipynb
[NbConvertApp] Converting notebook 2.4d_batchelor_nest.ipynb to script
[NbConvertApp] Writing 12503 bytes to ../../python/background/batchelor_nest.py
